1.2.3 Complex systems and chaos

The credibility of science lies in its ability to link cause and effect, and thus to make phenomena predictable. However, some systems exhibit random behaviour that seems to defy knowledge because of its complexity and unpredictability: turbulence, meteorology, population fluctuations, traffic jams, lethal arrhythmias and vascular accidents are just a few examples. These systems cannot be analysed using the classical methodology, which consists of looking for a single cause for each event by breaking it down into its simplest elements. The linear mathematical concept, which describes effects that are directly proportional to the intensity of their cause, no longer applies to these non-linear models, where it sees only chaos [8,10]. Non-linear systems are characterised by a seemingly unpredictable variability of effects: tiny causes can produce gigantic and unexpected results. They are also characterised by an overall behaviour that is different from that of its constituent elements; a complex system can cross certain thresholds, giving rise to emergent properties that are different from the initial properties of the system; an emergent property is a characteristic that is unpredictable at the local level but appears at the global level [23]. Nonlinear systems are also extremely dependent on initial conditions, defined as those at time zero of the observation. On the time scale, they tend to maintain adaptive variability but not stability [3]. Finally, the equations describing these nonlinear systems generally have no analytical solution [7]; only computer simulation can elucidate the possible behaviour of the system.

This new methodology has shown that these apparently chaotic behaviours are governed by elegant geometric structures that generate randomness as soon as the system under study has three or more degrees of freedom (or independent variables) and these follow, in whole or in part, exponential geometric progressions [4]. A simple example is a metal pendulum oscillating between three equidistant magnets; it will come to rest over one of the magnets after a complicated and disordered motion that could only be predicted if we knew with infinite precision the field of attraction of each magnet and the exact initial position of the pendulum, which is obviously impossible because of the limited precision of measurements and because the time zero of the experiment is not the time zero of the universe: we are intercepting a phenomenon that is already in progress [23]. Complex systems do not have to be complicated to give rise to innumerable possibilities in the midst of which they evolve in surprising ways. If we add a few grains to a pile of sand, the height of the pile increases, as does its slope; this slope increases up to a certain threshold, beyond which an avalanche is triggered. If we repeat this operation continuously, we see that the size of the avalanches is independent of the amount of sand added and that their frequency is inversely proportional to the logarithm of their size [23]. Finally, the term fractal is often associated with complexity and chaos; a fractal is a geometric concept describing an object composed of subunits whose structure is similar to that of the whole (Figures 1.6 and 1.7) [3,9]. These few points deserve to be developed in more detail in relation to biology.

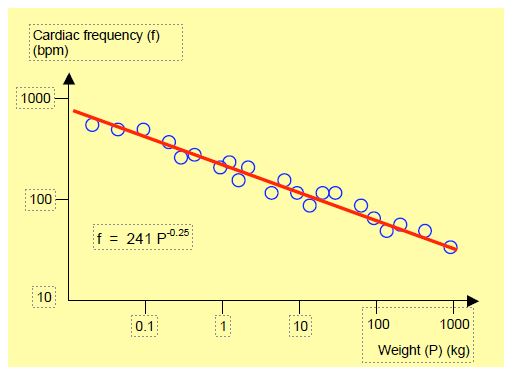
For centuries, sailors have described the sudden appearance of a monstrous wave in heavy weather; some capsized, many sank and a few came back. This rogue wave was considered a legend because it seemed extraordinary and because sailors definitely drink a lot. But in the second half of the 20th century, some cargo ships and oil tankers had time to send out an SOS before disappearing body and soul, describing themselves as facing a gigantic wall of water that was about to engulf them. The idea of modelling the dynamics of ocean waves on a computer and running the programme to generate billions and billions of waves led to the realisation that, from time to time, a veritable monster 25 metres high would appear. Satellite observations confirmed it. Small waves are common, large ones are rare and monumental ones are exceptional [15]. The same is true of earthquakes: their magnitude on the Richter scale (which is logarithmic) is directly related to the logarithm of their frequency; the relationship is a straight line whose slope is a fractal dimension (explained in Figures 1.6, 1.7 and 1.8). There is no difference in nature or cause between a large earthquake and a small one, or between a giant wave and a chop: only the intensity differs. The most significant events are simply rarer. You don't need a spectacular trigger to cause a disaster. In mathematics, the frequency of an event is equal to 1 divided by some power that defines the importance of the event. In other words, the magnitude of an event is equal to 1 divided by its frequency (f) raised to a certain power (P) that represents this magnitude: 1/f^P . In mammals, the increase in heart rate (f) in relation to the decrease in body mass (M) is also a straight line on a logarithmic scale (where f = 241 M^-0.25) (Figure 1.8) [21,22]. The same relationship exists between the magnitude of earthquakes and their frequency.

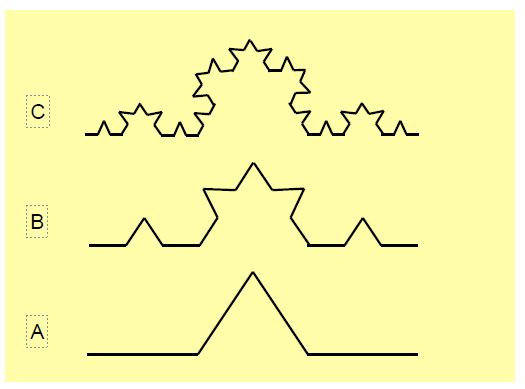
Figure 1.6: Construction of fractals (Koch curve). The central third of a straight line (A, bottom) is transformed into an isosceles triangle whose side is equal to the length of the third of the original straight line. This operation is repeated on the four segments of this line (B). It is repeated a second time to obtain the top image (C). You can repeat this operation as many times as you like: the total length of the curve obtained tends towards infinity even though its extremities are the same as those of the original segment and it does not rise any higher. To obtain the length of a side, divide the length of the primitive curve by 4 and multiply the result by 3 (see curve A). The power of 3 equal to 4 is 1.2619 (31.2619) [8]. The fractal dimension of the curve is 1.2619. The dimension of a fractal is always between 1 and 2. The fractal dimension of the coast of Norway with its tangled fjords, for example, is 1.52. In reality, the length measured depends on the scale chosen. If the map representing the coast of Norway is covered with a grid of small squares and the length of the coast is measured in each square, the smaller the squares chosen, the greater the total length. A graph comparing the logarithm of the length of coastline measured in each square (on the ordinate) and the logarithm of the size of the squares (on the abscissa) shows that the relationship is a straight line whose slope is the fractal dimension (see Figure 1.8). The product of the logarithms of the rib length and the square size is a constant: we say that there is scale invariance.

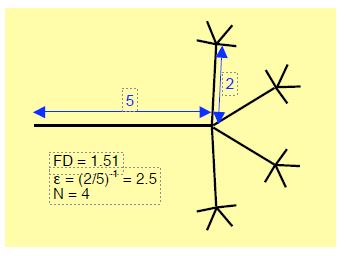
Figure 1.7: Theoretical fractal branching schematically illustrating a network of dendrites, coronary capillaries or subdivisions of Purkinje fibres. In this case, the fractal dimension (FD) is 1.51, the scale relating the size of the branches (ε) is (2/5)^-1 or 2.5 and the number of branches (N) is 4. Calculation of the fractal dimension: FD = log 4/log (5/2) = 1.51) [3].

Figure 1.8: Relationship between mammalian weight and heart rate. The smaller the animal, the higher the rate. The scale is logarithmic for both data [after Schmidt-Nielsen K. Animal physiology. 5th edition. Cambridge: Cambridge University Press, 2002, p 101]. The same type of line is obtained in other power laws, such as the relationship between the power of earthquakes or the height of waves and their frequency, the relationship between the quantity of DNA contained in a cell and the number of different cell types possessed by the living being in question, or the relationship between the scale of a geographical map and the length of a coastline. In the latter case, the slope of the line (its power) is a measure of the fractal dimension of the coastline.

The human genome contains between 30,000 and 100,000 genes that can interact by activating or deactivating each other (cross-talk) in a complex network of connections and feedbacks; these genes control the differentiation and cellular activity of our organism. We have 256 types of cells in our bodies. If we compare species from bacteria to humans, we can see that the number of cell types increases as a function of the square root of the number of genes [11]. In other words, the same rules that apply to waves, earthquakes and piles of sand also apply to the genes, cells and organs in our bodies. There is scale invariance; we are in a fractal system.

This power law (1/f^P ) always applies to complex systems made up of many components, open systems powered by an external energy source that spontaneously manage themselves in a self-organised critical state on the border between stability and chaos, and maintain themselves there in a dynamic and unstable equilibrium [10]. A good example is the network system, a set of points, sometimes connected in pairs, made up of several interdependent elements. In the brain, these elements are neurons connected by their dendrites, in the cell they are molecules connected by chemical reactions, and in society they are individuals connected by their social relationships. But in each of these systems, the probability that an element "e" is linked to k other elements is also a power law: 1/k^e. Depending on the number of links and the number of elements, the network can behave in a regular or random way, but if this number is large enough, the network is in a dynamic equilibrium around a position close to the transition between order and chaos [11]. It is then robust enough to withstand perturbations or broken connections, but it is also fundamentally unpredictable. Indeed, the number of possible combinations quickly becomes astronomical, even in a small network: with a thousand interconnected elements, each of which can be in two states (e.g. activated or deactivated), we obtain 10³⁰⁰ possible configurations [23]; this number is such that the age of the universe would be insufficient time for a super-powerful computer to calculate all the possible combinations.

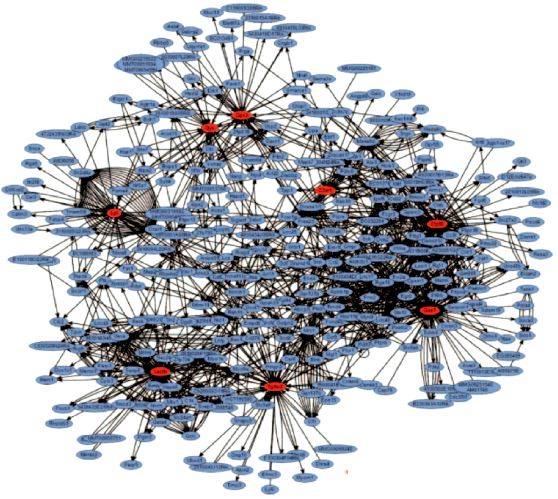
But something else happens in complex systems and networks. Certain combinations and certain connections recur more often than others. In networks, connections cluster around certain hubs, which centralise a maximum number of connections and whose function is a priority for the circulation of information (Figure 1.9) [13]. A pathophysiological phenomenon is a node that appears to us as an autonomous entity because we simplify reality to make it understandable and manipulable, neglecting the reticular aspect of reality and forgetting that each element is totally interdependent with those to which it is linked within the networks. To describe it in this way is to isolate the hub and analyse its operation independently of its many connections.

If we simulate our 30,000 known genes and their interconnections in a programme where each gene can be activated or inhibited, we obtain 10⁹⁰⁰⁰ possible combinations. This figure is obviously unachievable. However, if we run a computer simulation programme, we can see that the countless possibilities are condensed around a limited number of realisations or cyclic states, in this case 173. These foci of realisations have been called attractors; their number is equivalent to the square root of the number of elements (in this case the genes) [10,18]. Given that we have between 30,000 and 100,000 genes, it is intriguing to note that we have 256 different cell species, the probable number of attractors corresponding to the square root of the number of genes [10,23]. At the global level, complexity generates too many possibilities to be predictable, but appears to be profoundly self-organising.

Physiological rhythms such as heart rate, respiration or blood pressure are not strictly periodic, but exhibit constant non-linear variations that can be partially likened to fractals unfolding in time instead of space [7]. The anarchy of an arrhythmia or hyper-regularity due to loss of fluctuations both lead to pathology [14]. Complex fluctuations in cardiac rhythm are probably an essential physiological function ensuring greater robustness of the system in the face of environmental variations. The EEG is one of the most complex physiological signals. Non-linear mathematics is used clinically to analyse its pattern in different ways. Entropy quantifies the degree of randomness or impredictability of the signal (a simple sine wave has an entropy of 0, whereas anarchic noise has maximum entropy); normalised complexity quantifies the degree of repetition of identical sequences in a signal train; and the fractal dimension measures the increase in disparity in signal amplitude as sampling is spaced further and further apart [6]. All these techniques are used to analyse the EEG trace and extract information about the depth of sleep.

Figure 1.9: Image of networks contributing to genetic adiposity in mice. The hubs are the 8 red foci, each representing one of the genes involved in the disease [Lusis AJ, Weiss JN. Cardiovascular networks. Systems-based approaches to cardiovascular disease. Circulation 2010; 121:157-70].

Non-linear mathematical theories have shown that the limits of predictability are inherent in complex systems for two reasons. First, the extreme sensitivity to initial conditions of a system with multiple interdependencies determines its evolution and means that, through a cascade of events linked over time, tiny differences in the initial situation can lead to huge variations in the long-term results. Phenomena of dimensions unobservable on our scale take on, through exponential growth, values comparable to the magnitudes that express the initial state of the system. Whatever the precision of the measurements of the initial state, it cannot be infinite, so there is always some uncertainty. Secondly, the growth of these uncertainties is exponential as the system evolves: each measurement is subject to errors, and these errors grow so rapidly that any prediction becomes impossible. The butterfly effect has been described in this way: it can be calculated that the flapping of a butterfly's wings, a tiny event if ever there was one, has the effect, after some time, of changing the state of the Earth's atmosphere and its meteorology in unpredictable ways [18]. In fluid physics, it takes only one day for changes of the order of a centimetre to become changes of the order of ten kilometres [19]. There is an intriguing analogy here with the nadir of myocardial performance that occurs 5-6 hours after bypass surgery [17], or with postoperative cardiac complications, the incidence of which is highest between the 2nd and 3rd postoperative day [12]. Perhaps they are the consequence of a series of minute changes that began during the operation but which our measuring instruments cannot detect at that time. There is also a worrying analogy with the genesis of accidents: in complex systems, apparently harmless gestures can have unfortunate consequences through progressive amplification. These gestures may even be everyday occurrences, and then, exceptionally, end up being associated with a catastrophe because chance has changed the context.

Initial conditions are defined as those at time zero of the observation, but the system itself is constantly evolving over time: each instant represents the initial conditions of another sequence of events, itself the inheritance of a previous situation. What's more, a complex system can cross certain thresholds, giving rise to emergent properties that are different from the initial properties of the system; for example, below a certain temperature, water crystallises and ice takes on properties not present in the aqueous phase; this is a phase transition. If grains of sand are added to or subtracted from an almost flat pile, the neighbouring grains remain unchanged and nothing happens. But if the pile is high and has a fairly steep slope, removing or adding a single grain will throw the whole thing out of balance and the whole slope will change as the pile collapses. Increasing the slope of the pile is equivalent to increasing the interdependence of the grains, like adding connections to a set of units. Systems that are complicated enough to give rise to emergent properties, yet stable enough to be observed, are those in which each element is connected to a set of two to five others, and has feedback relationships with them that can be catalysing or inhibiting. This phenomenon may provide an explanation for the origin of life. In the primordial soup of amino acids from which life emerged, a network of links was established between chemical substances that reacted with each other; some reactions were autocatalytic and self-sustaining, while others were inhibitory and slowed down the formation of certain molecules. A very plausible hypothesis is that life represents a phase transition in a chemical system with a sufficient number of network connections. A few fewer links and nothing happens, a few more and life becomes inevitable [10]. This may not be a coincidence, but a necessity.

Since a difference in scale leads to a difference in properties, the decomposition of a complex system into simpler units that can be added together does not allow the functioning of the whole to be explored when organisational thresholds are crossed. A particularly dense interactive network of neurons can bring sensory stimulation to a state of consciousness above a certain threshold of complexity [20]. Individual variability disappears on a collective scale, not because of the cumulative effect of a large number of different units, but because there is a progressive homogenisation of units in relation to each other; cooperative behaviour therefore emerges between individualised units [1]. Hence the title of a famous article in Science: "More is different" [2]. Individual variability is not just a parasitic phenomenon that disturbs the existing determinism. On the contrary, it is the very source of the emergence of new properties, acting as a nucleus of crystallisation around which the whole can be restructured in a new dimension through synergy rather than accumulation. Such a paradigm may seem vague to classical mechanical physics, but it is the epistemological basis of modern biology and neurophysiology.

To complicate matters, complex systems are dynamic; operations are repeated over and over again, like the oscillation of a pendulum or the beating of a heart. Mathematical analysis of these repetitions and their variability reveals that it is the smallest fluctuations that ultimately dominate the system as a whole, while the system demonstrates the ability to constantly rebalance itself to mitigate the effects of gross changes imposed by the environment [4]. The concept of chaos challenges the reductionist idea of analysing the behaviour of a system by reducing it to that of its constituent elements; it imposes the idea that its long-term evolution is unpredictable because variability is part of its nature. The only system capable of simulating a complex event in all its detail is the event itself. In the context of predicting the risk of surgery and analysing the fate of anaesthetic patients, these logical concepts shed new light on the difficulties encountered over the last twenty years in researching the determinants of risk and the factors triggering morbidity and mortality. Their indeterminate and random nature precludes reliable individual predictions for each patient. It is also understandable that the results of randomised controlled clinical trials, which isolate certain data to be observed in a highly selected population, are never confirmed with the same significance by studies carried out in the real clinical world, where multiple confounding factors are constantly at play.

We know this from meteorology: even if we knew all the elements at play at any given time, we could only make reliable predictions in the short term. Dynamic or chaotic systems can be studied at two levels: that of individual trajectories, which illustrate disorder, and that of ensembles, which are described by probability distributions and exhibit analysable behaviour at this scale [16]. Perfect knowledge of the factors involved in myocardial ischaemia would therefore only allow probabilistic prediction: it would be possible to define whether a patient belongs to a class with a defined probability of having an infarction, but it would still be impossible to know whether that particular patient would have an infarction or not. Because causality is not linear, but multifactorial and redundant, we can only predict risks or chances in relation to a group of individuals. Patients, on the other hand, are in a binary system: they are either alive or dead; they have only two possibilities: 0% or 100%. Conversely, the fact that this particular patient did not suffer a heart attack during anaesthesia does not change the risk associated with this class of patient, nor does it in any way validate the technique used; the probability of an event remains the same whether the event occurred or not. An isolated success does not prove anything!

Another aspect of the phenomena must also be considered. In living systems, errors and perturbations occur all the time, although their effects are attenuated by the organism's homeostatic systems, which tend to maintain equilibrium in the face of deviations. All these systems contain multiple constraints that can reinforce or cancel each other out, depending on the circumstances. Thus, the fate of an atheromatous plaque depends on the momentary balance of lipids and inflammatory cells it contains, its endothelial capsule, current unbalancing factors (smoking, stress) or stabilising substances (e.g. statins), platelet activity and fibrinolysis, local shear forces (arterial hypertension) and endothelial activity (abnormal in atheromatous disease), diet and genetic make-up. A thrombus may be evacuated by flow, rapidly lysed or enlarged by hypercoagulability. The survival of the distal myocardium depends on its current oxygen demand (exercise or rest, tachycardia or bradycardia, presence of valvular disease), oxygen supply (hypoxia, hypotension, low flow, anaemia or hyperviscosity) and the degree of collateralisation. If we look at the cellular level, we can see, for example, that 1-2% of the electrons passing through the oxidation-reduction chain in the mitochondria escape into the cytoplasm to form toxic superoxides, which are generally lysed by enzymes (super-O^{- -}dismutases). The DNA of each of our cells is subjected to 10,000 of these oxidative attacks every day, some of which lead to mutations [5]; and this damage accumulates with age. The survival of each of our cells is the result of a dynamic balance between the factors that condition its growth and those that control its apoptosis. Apoptosis is programmed by genes activated by metabolic stress or ischaemia.

This very partial enumeration of the multiple phenomena at play simultaneously reflects the fundamental unpredictability of an event, especially one as complex and variable as a plane crash or a heart attack. It is illusory to try to reduce them to a few simple causes, to classify them into precise categories, each with its own therapy, and to believe that the importance of the effect is proportional to that of the cause. Faced with this diversity, our treatments are crude, but they work in a significant proportion of cases. We simply consider them adequate if we are satisfied with their probability of being right.

© PG Chassot  April 2007, last update September 2019

References

1. AMZALLAG GN. La raison malmenée. Paris, CNRS Edition, 2002
2. ANDERSON PW. More is different. Science 1972; 177:393-6
3. CAPTUR G, KARPERIEN AL, HUGHES AD, et al. The fractal heart – embracing mathematics in the cardiology clinic. Nat Rev Cardiol 2017; 14: 56-64
4. CRUTCHFIELD J, FARMER D, PACKARD N, SHAW R. Le chaos. In: DE GENNES PG. L'ordre du chaos. Pour la Science, Diffusion Belin, Paris, 1992, pp 34-51
5. DAS DK, MAULIK N. Mitochondrial function in cardiomyocytes: target for cardioprotection. Curr Opinion Anesthesiol 2005; 18:77-82
6. FERENETS RM, VANLUCHENE A, LIPPING T, et al. Behavior of entropy/complexity measures of the EEG during propofol-induced sedation : dose-dependent effects of remifentanil. Anesthesiology 2007; 206:696-706
7. GLASS L. Synchronization and rhythmic processes in physiology. Nature 2001; 410:277-84
8. GOLDBERGER AL. Non-linear dynamics for clinicians: chaos, fractals, and complexity at the bedside. Lancet 1996; 347:1312-4
9. GOLDBERGER AL, RIGNEY DR, WEST BJ. Chaos and fractals in human physiology. Sci Am 1990; 262:42-9
10. GRIBBIN J. Simplicité profonde. Le chaos, la complexité et l’émergence de la vie. Paris, Flammarion, 2006
11. KAUFMAN S. At home in the Universe. The search for the laws of self-organisation and complexity. New York, Oxford University Press, 1995
12. LE MANACH Y, PERREL A, CORIAT P, et al. Early and delayed myocardial infarction after abdominal aortic surgery. Anesthesiology 2005; 102: 885-91
13. LUSIS AJ, WEISS JN. Cardiovascular networks. Systems-based approaches to cardiovascular disease. Circulation 2010; 121:157-70
14. MUZI M, EBERT TJ. Quantification of heart rate variability with power spectral analysis. Curr Opinion Anesthesiol 1993; 6:3-17
15.  OLAGNON M.  Rogue Waves: Anatomy of a Monster  (Adlard Coles Nautical, 2017)
16. PRIGOGINE I. Les lois du chaos. Flammarion, Paris, 1994, p 10
17. ROYSTER RL. Myocardial dysfunction following cardiopulmonary bypass: Recovery patterns, predictors of initropic needs, theoretical concepts of inotropic administration. J Cardiothor Vasc Anesth 1993; 7(Suppl 2):19-25
18. RUELLE D. Hasard et chaos. Ed. Odile Jacob, Paris, 1991, p 99
19. RUELLE D. Déterminisme et prédicibilité. In: DE GENNES P.G. - L'ordre du chaos. Pour la Science, Diffusion Belin, Paris, 1992, pp52-63
20. SACKS O. Les instantanés de la conscience. La Recherche 2004; 374:30-8
21. SCHMIDT-NIELSEN K. Animal physiology. 5^th edition. Cambridge, Cambridge University Press, 2002; 101
22. STAHL VR. Scaling of respiratory variables in mammals. J Appl Physiol 1967; 22:453-60
23. ZWIRN HP. Les systèmes complexes. Mathématiques et biologie. Paris: Odile Jacob, 2006